Many of us have seen an ant walking across a table, wandering this way and that. Some may just stare at it for a while and then move on, but others will wonder "Why does it move in the way that it does?" I am not a biologist, so I would not know the answer. However, there is a way to use simple rules to simulate something similar to an ant's complex behavior - Langton's Ant.
Langton's ant is simulated with an "ant" on an infinite grid of white squares. When it is on a white square, it makes it black, turns right, and moves one square in the direction that it's facing. If it's on a black square, it turns it white and goes to the left. Here is an animation showing the ant's first 200 steps:
Langton's ant is simulated with an "ant" on an infinite grid of white squares. When it is on a white square, it makes it black, turns right, and moves one square in the direction that it's facing. If it's on a black square, it turns it white and goes to the left. Here is an animation showing the ant's first 200 steps:
It seems like chaotic behavior, but after about 11000 steps, it begins to fall into a repetitive pattern, moving across the board and leaving a trail, or "highway", behind it.
It isn't super interesting, but the rules of the ant can be changed. The current rule can be written as RL, because when the ant lands on color 0 (white), it turns right, and when it's on color 1 (black), it turns left. Whenever the ant lands on color n, it changes it to color n+1, and if it's run out of colors (e.g. color 6 when it only goes up to 5), it resets it to color 0. (F and B can also represent forward and backward for the ant.)
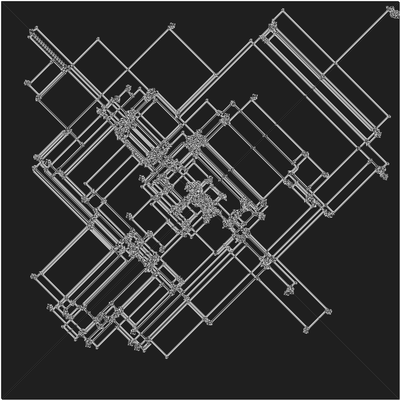
Another rule is rule LRL. When the ant reaches color 0 (white), it makes it color 1 (black) and turns left. If it's on color 1, it changes it to color 2 (grey) and goes to the right. Finally, if the ant lands on color 2, it turns left and makes it color 0 again. This rule is extremely chaotic, and it is unknown if it ever creates a highway. Here is what it looks like after reaching the edge of a 1000-by-1000-cell box.
Another rule is rule LRL. When the ant reaches color 0 (white), it makes it color 1 (black) and turns left. If it's on color 1, it changes it to color 2 (grey) and goes to the right. Finally, if the ant lands on color 2, it turns left and makes it color 0 again. This rule is extremely chaotic, and it is unknown if it ever creates a highway. Here is what it looks like after reaching the edge of a 1000-by-1000-cell box.
There are many, many other behaviors that the ants can exhibit. Here are just a few.
(Some of the images are cut off, though.)
(Some of the images are cut off, though.)
1. LLRL: Produces a highway, similar to Langton's Ant, but not essentially the same.
2. RRLL: Grows into a cardioid shape.
3. LRRRRRLLR: Creates a growing square around itself, filled with chaotically bouncing highways.
4. LRRRRLLLRRR: Falls into a pattern of making Archimedes' spiral, surrounded by a solid square of cells.
5. RLLLLRRRLLLR: Similar to #4, but makes a logarithmic spiral instead.
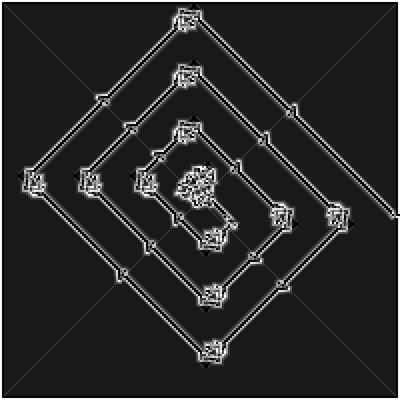
6. LF: Counts in binary. The number is mirrored along right and left sides. Any sequence of L's and then an F will count in different bases, depending on the number of L's.
There is even an extension of Langton's ant that follows different rules depending on what state it's in, called a Turmite, but I won't be able to post about it until I figure out the rule notation.
All images on this page, except for the first animation, were made with the following Processing program:
2. RRLL: Grows into a cardioid shape.
3. LRRRRRLLR: Creates a growing square around itself, filled with chaotically bouncing highways.
4. LRRRRLLLRRR: Falls into a pattern of making Archimedes' spiral, surrounded by a solid square of cells.
5. RLLLLRRRLLLR: Similar to #4, but makes a logarithmic spiral instead.
6. LF: Counts in binary. The number is mirrored along right and left sides. Any sequence of L's and then an F will count in different bases, depending on the number of L's.
There is even an extension of Langton's ant that follows different rules depending on what state it's in, called a Turmite, but I won't be able to post about it until I figure out the rule notation.
All images on this page, except for the first animation, were made with the following Processing program:
| langton.pde | |
| File Size: | 2 kb |
| File Type: | pde |